การนำกฏทั้งสองของเคอร์ชอฟฟ์ มาแก้ปัญหาในวงจรสามารถทำได้ดังนี้
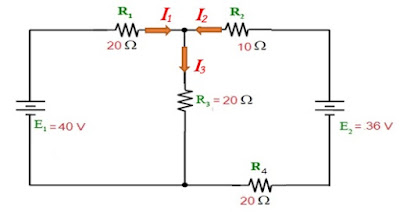
ตัวอย่าง จากวงจรด้านล่าง จงหากระแสที่ไหลผ่านความต้านทานแต่ละตัวโดยใช้กฏของเคอร์ชอฟฟ์
วิธีทำ
1. กำหนดกระแสไหลในวงจร (ปกติจะกำหนดให้ไหลออกจากขั้วบวกของแหล่งจ่ายไฟฟ้า)
2. เขียนสมการกระแสของเคอร์ชอฟฟ์ จากกระแสที่สมมติขึ้น
จะได้ I3 = I1 + I2
3. เขียนสมการแรงดันของเคอร์ชอฟฟ์ ในวงจรปิดด้านซ้ายมือ
จะได้ V1 + V3 = E1
จากกฎของโอห์ม V = IR จะได้
V1 = I1R1
V3 = I3R3
แทนค่าในสมการแรงดันของเคอร์ชอฟฟ์ จะได้
I1R1 + I3R3 = E1
แทนค่าที่รู้ลงในสมการ จะได้
20I1 + 20I3 = 40
4. แทนค่า I3 = I1 + I2 ลงในสมการแรงดันของเคอร์ชอฟฟ์ จะได้
20I1 + 20 ( I1 + I2 ) = 40
20I1 + 20I1 + 20I2 = 40
40I1 + 20I2 = 40............ ...①
สมการที่ 1 หาร 20 , 2I1 + I2 = 2............ ...②
5. เขียนสมการแรงดันของเคอร์ชอฟฟ์ ในวงจรปิดด้านขวามือ
จะได้ V2 + V3 + V4 = E2
จากกฎของโอห์ม V = IR จะได้
V2 = I2R2
V3 = I3R3
V4 = I2R4
แทนค่าในสมการแรงดันของเคอร์ชอฟฟ์ จะได้
I2R2 + I3R3 + I2R4 = E2
แทนค่าที่รู้ลงในสมการ จะได้
10I2 + 20I3 + 20I2 = 36
6. แทนค่า I3 = I1 + I2 ลงในสมการแรงดันของเคอร์ชอฟฟ์ จะได้
10I2 + 20 ( I1 + I2 ) + 20I2 = 36
10I2 + 20I1 + 20I2 + 20I2 = 36
นำค่ากระแสเหมือนกันมารวมกัน จะได้
20I1 + 50I2 = 36............ ...③
สมการที่ 3 หาร 2 , 10I1 + 25I2 = 18............ ...④
7. นำสมการที่ 2 และ 4 ไปหาค่าตัวแปร I1 และ I2 ด้วยวิธีตามที่นักเรียนถนัด
2I1 + I2 = 2............... ②
10I1 + 25I2 = 18............. ④
แก้สมการโดยใช้แมทตริก จะได้
I1 = DI1 / D
= 32 ÷ 40
= 0.8 A
I2 = DI2 / D
= 16 ÷ 40
= 0.4 A
ดังนั้นจะได้
กระแสที่ไหลผ่าน R1 IR1 = I1 = 0.8 A
กระแสที่ไหลผ่าน R2 IR2 = I2 = 0.4 A
กระแสที่ไหลผ่าน R3 IR3 = I3
= I1 + I2
= 0.8 + 0.4 = 1.2 A








ความคิดเห็น