กฏของเคอร์ชอฟฟ์

จำนวนผู้เยี่ยมชมหน้านี้

             กฏของเคอร์ชอฟฟ์ เป็นกฎในการคิดคำนวณค่าทางไฟฟ้า ในวงจรที่มีความยุ่งยาก เกินกว่าที่จะใช้กฏของโอห์ม ในการคำนวณ

             กฏของเคอร์ชอฟฟ์ แบ่งออกเป็น 2 กฏ คือ
             1. กฏกระแสของเคอร์ชอฟฟ์ (Kirchhoff's Current Law : KCL) กล่าวไว้ว่า 

"ผลรวมทางพีชคณิตของกระแสไฟฟ้า ณ จุดใดๆ จะมีค่าเท่ากับศูนย์"     หรือ 

"ผลรวมของกระแสไฟฟ้าที่ไหลเข้าจุดใดๆ จะเท่ากับผลรวมของกระแสไฟฟ้าที่ไหลออกจุดนั้น"

ภาพที่ 1 แสดงกระแสไฟฟ้าที่จุดๆ หนึ่ง

                           จากรูปด้านบน เราสามารถเขียนกฎกระแสของเคอร์ชอฟฟ์ ได้ดังนี้

                                I₁ - I₂ + I₃ - I₄ - I₅ = 0     หรือ

                                                  I₁ + I₃  = I₂ + I₄ + I₅

              จากในภาพเราสามารถหาค่ากระแสที่ไม่รู้ค่าคือ  I₅  ได้ ดังนี้       

          - ย้ายค่าที่ทราบไปอยู่ทางขวามือของสมการ จะได้

                     I₅ =  I₁ + I₃ - I₂ - I₄

          - แทนค่าที่ทราบลงในสมการ จะได้ 

                     I₅ =  5 + 8 - 2 - 7

                         =  4 A                  

             2. กฏแรงดันของเคอร์ชอฟฟ์ (Kirchhoff's Voltage Law : KVL) กล่าวไว้ว่า 

"ผลรวมทางพีชคณิตของแรงดันไฟฟ้าทั้งหมดในวงจรไฟฟ้าปิดใดๆ จะทีค่าเท่ากับศูนย์" หรือ 

"ผลรวมของแรงดันไฟฟ้าที่ตกคร่อมความต้านทานในวงจรนั้นจะมีค่าเท่ากับแรงดันไฟฟ้าที่จ่ายให้กับวงจรนั้น"

ภาพที่ 2 แสดงวงจรไฟฟ้าปิดลูปใดๆ 

              จากรูปด้านบน เราสามารถเขียนสมการโดยใช้กฎแรงดันของเคอร์ชอฟฟ์ ได้ดังนี้

                  ผลรวมทางพีชคณิตของแรงดันไฟฟ้าในวงจรไฟฟ้าปิดใดๆ จะเท่ากับศูนย์ (โดยให้แรงดันที่จ่ายมีค่าเป็นบวก และแรงดันที่ตกคร่อมที่ตัวต้านทานมีค่าเป็นลบ)
                       E₁ - V₁ - V₂ - V₃ - V₄  = 0    

 หรือ ผลรวมของแรงดันไฟฟ้าที่ตกคร่อมความต้านทานในวงจรนั้นจะเท่ากับแรงดันไฟฟ้าที่จ่ายให้กับวงจรนั้น
                            V₁ + V₂ + V₃ + V₄  =  E₁  

ในวงจรปิด ภาพที่ 2 จะได้

V₁ = IR₁
V₂ = IR₂
V₃ = IR₃
V₄ = IR₄

แทนค่า ในสูตร จะได้

IR₁ + IR₂ +  IR₃ + IR₄ = 150

30I + 10I + 15I + 20I = 150

                             75I = 150

                                 I = 150 / 75

                                   = 2 A
จะได้กระแสไฟฟ้าไหลในวงจรเท่ากับ 2 แอมป์

             การนำกฏทั้งสองของเคอร์ชอฟฟ์ มาแก้ปัญหาในวงจรสามารถทำได้ดังนี้
 
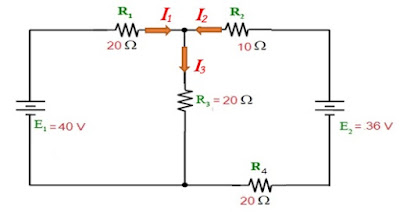
            ตัวอย่าง  จากวงจรด้านล่าง จงหากระแสที่ไหลผ่านความต้านทานแต่ละตัวโดยใช้กฏของเคอร์ชอฟฟ์

                     วิธีทำ  

           1. กำหนดกระแสไหลในวงจร (ปกติจะกำหนดให้ไหลออกจากขั้วบวกของแหล่งจ่ายไฟฟ้า)

            2. เขียนสมการกระแสของเคอร์ชอฟฟ์ จากกระแสที่สมมติขึ้น  

                           จะได้     I₃  =  I₁ +  I₂   

                   3. เขียนสมการแรงดันของเคอร์ชอฟฟ์ ในวงจรปิดด้านซ้ายมือ 

                           จะได้   V₁ +  V₃  =  E₁

                                       

                    จากกฎของโอห์ม  V = IR    จะได้ 

                                                 V₁ = I₁R₁

                                                V₃ = I₃R₃              

                     แทนค่าในสมการแรงดันของเคอร์ชอฟฟ์  จะได้

                                                  I₁R₁ +  I₃R₃  = E₁

                    แทนค่าที่รู้ลงในสมการ  จะได้ 

                                                   20I₁ +  20I₃  = 40

          4. แทนค่า   I₃ = I₁  +  I₂    ลงในสมการแรงดันของเคอร์ชอฟฟ์  จะได้

                                               20I₁ +  20 ( I₁ + I₂ )  =  40

                                              20I₁ +  20I₁ +  20I₂   = 40

                                                        40I₁  +   20I₂   =  40............ ...①

                สมการที่ 1 หาร 20 ,                2I₁  +  I₂  =  2............ ...②

       

       5. เขียนสมการแรงดันของเคอร์ชอฟฟ์ ในวงจรปิดด้านขวามือ 

                           จะได้   V₂  +  V₃   +  V₄  =  E₂

                                       

                    จากกฎของโอห์ม  V = IR    จะได้ 

                                                 V₂  =  I₂R₂

                                                 V₃  = I₃R₃ 

                                                 V₄ = I₂R₄

                     แทนค่าในสมการแรงดันของเคอร์ชอฟฟ์  จะได้

                                                  I₂R₂  +   I₃R₃  +  I₂R₄  =  E₂

                    แทนค่าที่รู้ลงในสมการ  จะได้ 

                                                   10I₂  +  20I₃  +  20I₂  =  36

         6. แทนค่า  I₃  =  I₁  +  I₂  ลงในสมการแรงดันของเคอร์ชอฟฟ์  จะได้

                                              10I₂  +  20 ( I₁ +  I₂ )  +  20I₂  =  36

                                               10I₂  +  20I₁ +  20I₂  +  20I₂  =  36

                   นำค่ากระแสเหมือนกันมารวมกัน จะได้

                                                            20I₁ +  50I₂  = 36............ ...③

                สมการที่ 3 หาร 2 ,              10I₁ +  25I₂  = 18............ ...④

                      7. นำสมการที่ 2 และ 4  ไปหาค่าตัวแปร  I₁ และ  I₂  ด้วยวิธีตามที่นักเรียนถนัด

                                                 2I₁  +   I₂  =  2............... ②

                                           10I₁   +  25I₂  = 18............. ④

              

               แก้สมการโดยใช้แมทตริก จะได้

\   I₁   =  DI₁ / D

              = 32 ÷ 40

              = 0.8 A

        I₂   =  DI₂ / D

              = 16 ÷ 40

              = 0.4 A

  ดังนั้นจะได้

        กระแสที่ไหลผ่าน R₁                          I_R1 = I₁ = 0.8 A

        กระแสที่ไหลผ่าน R₂                          I_R2 = I₂ = 0.4 A

        กระแสที่ไหลผ่าน R₃                          I_R3 =  I₃

                                                                         =  I₁ +  I₂

                                                                         = 0.8 + 0.4 = 1.2 A